Finite Impulse Response Filtering

date:: 31 oct 2019

Continuous Fourier Transform

\[\begin{split}\begin{align*} & \boxed{x\leftrightarrow k={2\pi\over \lambda} \qquad t\leftrightarrow \omega={2\pi\over T}=2\pi f} \\ & \tilde{f}(k)={1\over\sqrt{2\pi}} \int_{-\infty}^{\infty} e^{-ikx}f(x)dx\\ & f(x)={1\over\sqrt{2\pi}} \int_{-\infty}^{\infty} e^{ikx}\tilde{f}(k)dk\\ & f(x)*g(x)=\int_{-\infty}^{\infty}f(y)g(x-y)dy \\ & F\{f(x)*g(x)\} =\sqrt{2\pi} \tilde{f}(k)\tilde{g}(k)\\ &\sqrt{2\pi} F\{f(x)g(x)\} = \tilde{f}(k)*\tilde{g}(k)\\ \end{align*}\end{split}\]

Discrete Fourier Transform

In actual implementations of DFT (numpy, tensorflow…), the algorithm doesn’t have to know about \(\boxed{dx}\), since it cancels out in various places
In the following, I leave the expression Unsimplified Intentionally , so we can get a better understanding by mapping to the Continuous Fourier Transform

\[\begin{split}\begin{align*} &\boxed{\text{discrete}} &\boxed{\text{continuous}} \\ & F_m=\sum\limits_{n=0}^{N-1} e^{-i(m{2\pi\over Ndx})ndx} f_n \cdot 1={F_{\text{m}}^{\text{true}}\over dx}& \tilde{f}(k)={1\over\sqrt{2\pi}} \int_{-\infty}^{\infty} e^{-ikx}f(x)dx \\ & f_n= {1\over2\pi} \sum\limits_{m=-N/2}^{N/2} e^{i(m{2\pi\over Ndx})ndx} (F_mdx) \cdot {2\pi\over Ndx} & f(x)={1\over\sqrt{2\pi}} \int_{-\infty}^{\infty} e^{ikx}\tilde{f}(k)dk \\ & \boxed{ f_n= \sum\limits_{m=-N/2}^{N/2} ... =\sum\limits_{m=0}^{N-1} ... } \\ & \boxed{F_{\text{m}}^{\text{true}}\to \tilde{f}(k) \quad Ndx\to \lambda \quad } \\ & \textbf{[note]}\; f(x)=\begin{cases} & \text{something} & x\in(0,\lambda) \\ & 0& \text{elsewhere}\\ \end{cases}\\ \end{align*}\end{split}\]

Signal Filtering

Suppose we have frequency domain ditribution \(\tilde{A}(\omega)\), that is, the amplitude of frequency \(\omega\)
And suppose we want to keep frequency below \(\omega_1\)
Thus we want

\[\begin{split}\begin{align*} & \tilde{A}'(\omega)=\begin{cases} & \tilde{A}(\omega) & \text{if } |\omega|<\omega_1\\ & 0 & \text{otherwise} \end{cases}=\tilde{A}(\omega)\; \text{rect}({\omega\over 2\omega_1}) \\ &\Rightarrow A'(t)={1\over \sqrt{2\pi}}A(t)* F^{-1}\{\text{rect}({\omega\over 2\omega_1})\} \\ & \quad ={1\over \sqrt{2\pi}}A(t)* {1\over\sqrt{2\pi}} 2\omega_1 \text{sinc}({\omega_1 t\over \pi}) \\ & \quad ={\omega_1\over \pi}A(t)* \text{sinc}({\omega_1 t\over \pi}) \\ & \boxed{\text{Low pass: }F^{-1}\{\text{rect}({\omega\over 2\omega_1})\}={1\over\sqrt{2\pi}} 2\omega_1 \text{sinc}({\omega_1 t\over \pi}) } \\ & \boxed{\text{Band pass: }F^{-1}\{\text{rect}({\omega\over 2\omega_\text{High}})- \text{rect}({\omega\over 2\omega_\text{Low}})\}} \\ & \boxed{\text{High pass: }F^{-1}\{1-\text{rect}({\omega\over 2\omega_\text{High}})\}=\sqrt{2\pi} \delta(x)-... } \\ & \text{we used}\\ & F^{-1}\{\text{rect}({\omega\over 2\omega_1})\} ={1\over\sqrt{2\pi}} \int_{-\omega_1}^{\omega_1} e^{i\omega t}d\omega={1\over\sqrt{2\pi}} {2\omega_1\over 2\omega_1 it}(e^{i\omega_1 t}-e^{-i\omega_1 t}) \\ & ={1\over\sqrt{2\pi}} 2\omega_1 \text{sinc}(\omega_1 t) \quad \text{unnormalized sinc function in physics}\\ & ={1\over\sqrt{2\pi}} 2\omega_1 \text{sinc}({\omega_1 t\over \pi}) \quad \text{normalized sinc function in numpy}\\ \end{align*}\end{split}\]

Homemade VS Numpy Fourier Transform

import numpy as np
import matplotlib.pyplot as plt

N = 1000; dx = 0.05; Lambda = N*dx
x = np.linspace(0,Lambda,N)
k = 2*np.pi/Lambda*np.arange(-N/2,N/2)

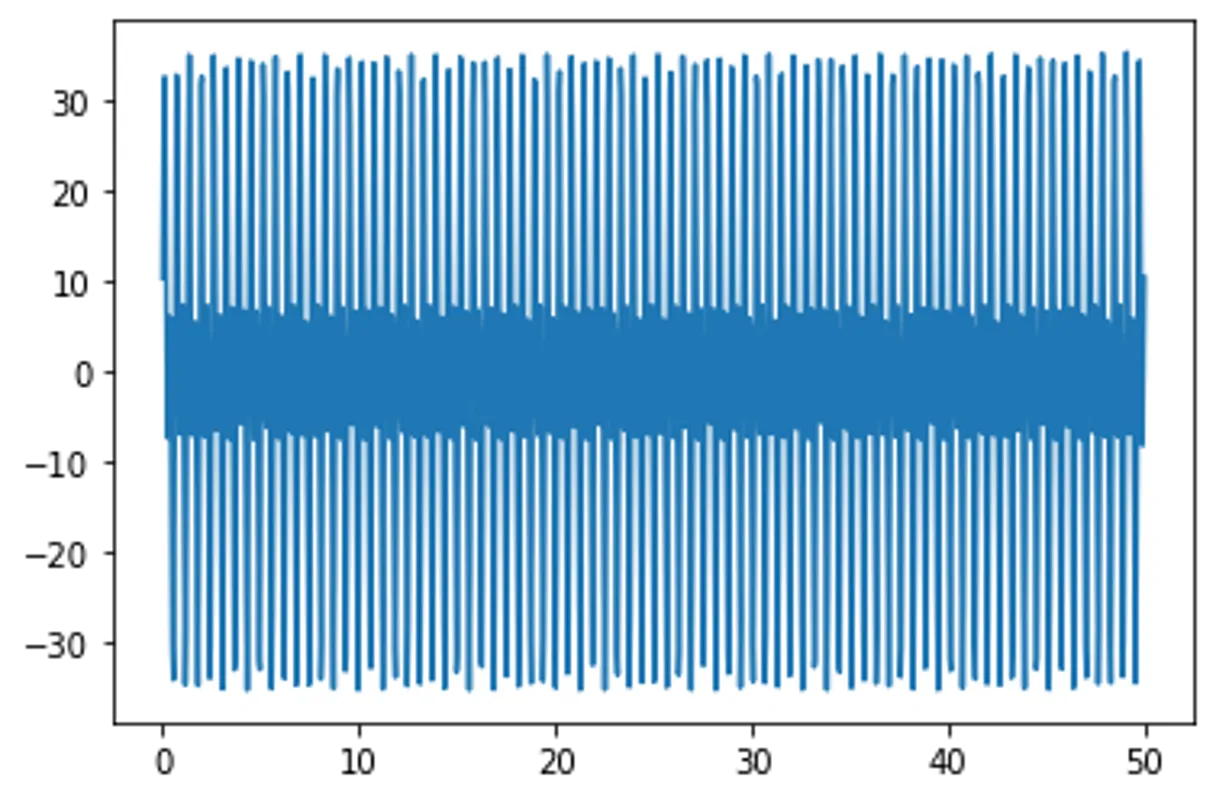
f_x = np.sin(10*x) + np.sin(20*x) + np.sin(40*x)

# homemade
F_k_homemade = []
for ki in k:
  F_k_homemade.append(np.sum( np.exp(-1j*ki*x)*f_x ))
F_k_homemade = dx*np.array(F_k_homemade)
plt.title("homemade DFT"); plt.plot(k, np.abs(F_k_homemade)); plt.show()

# numpy
F_k_numpy = dx*np.fft.fft(f_x)
F_k_numpy = np.concatenate((F_k_numpy[int(N/2):],F_k_numpy[:int(N/2)] ))
plt.title("numpy DFT"); plt.plot(k, np.abs(F_k_numpy)); plt.show()

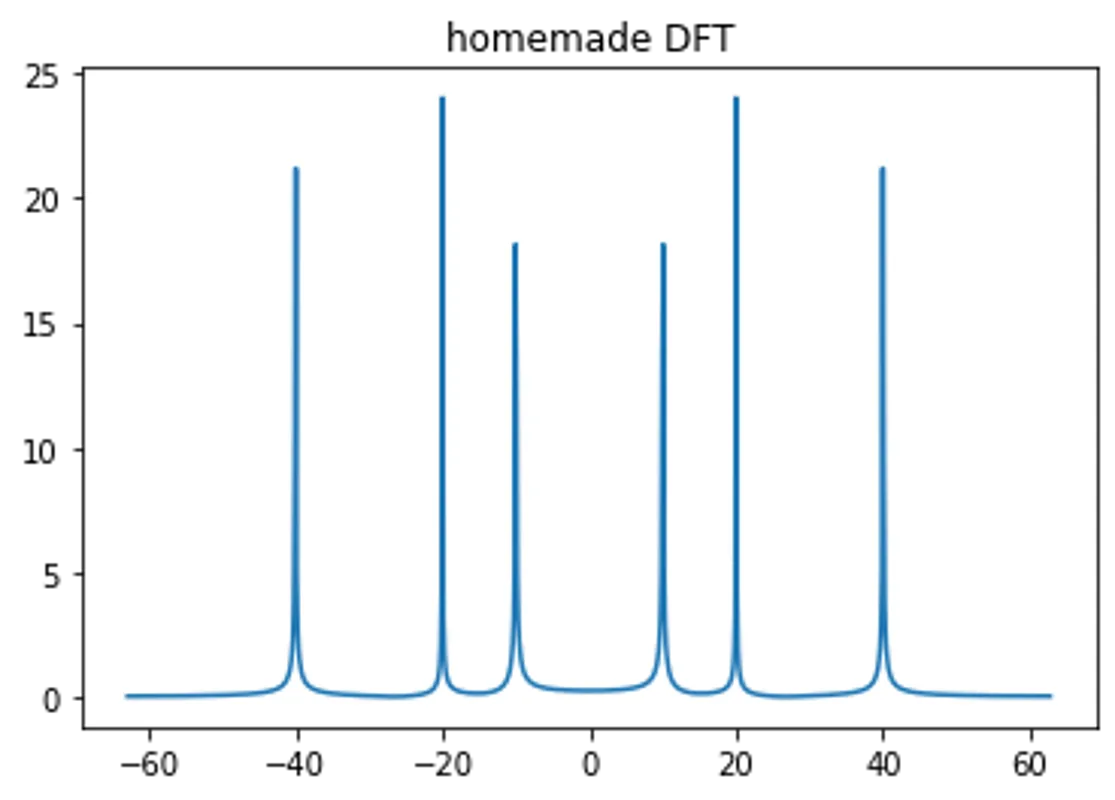
../_images/Finite-Impulse-Response-Filtering-output_3_0.webp

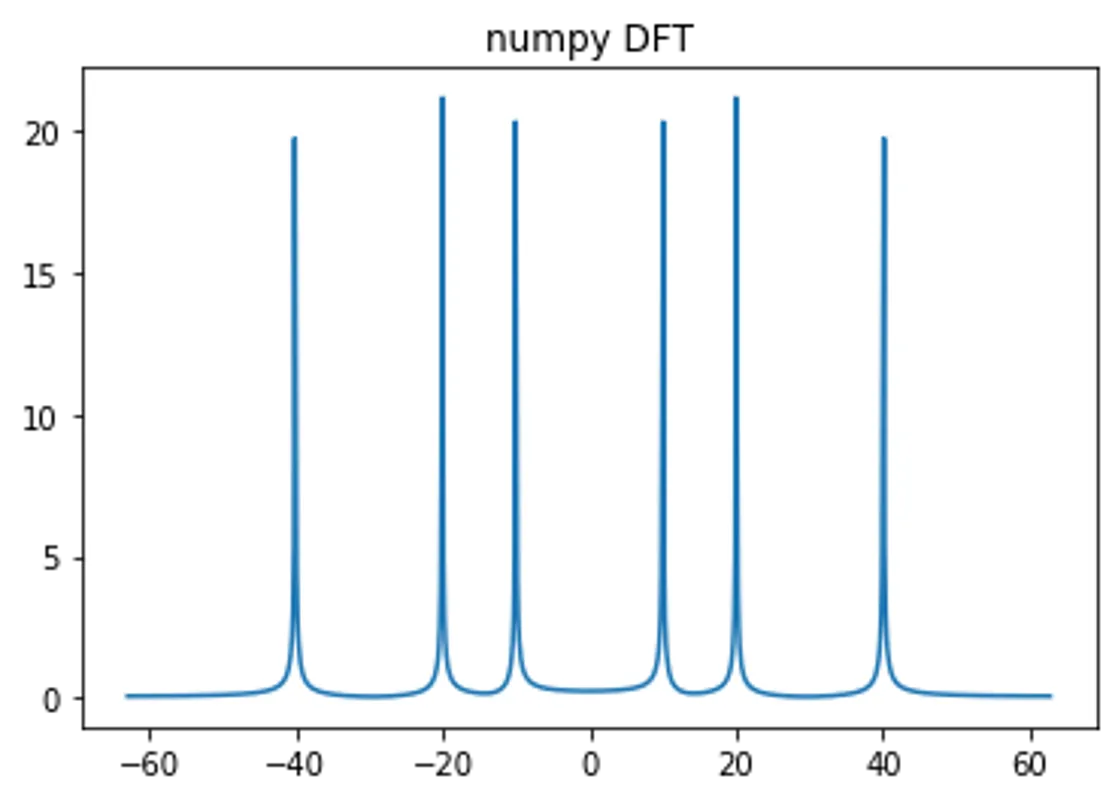
../_images/Finite-Impulse-Response-Filtering-output_3_1.webp

Homemade VS Numpy Filtering (Convolution)

k1=30

# homemade
f_x_filtered = []
for xi in x:
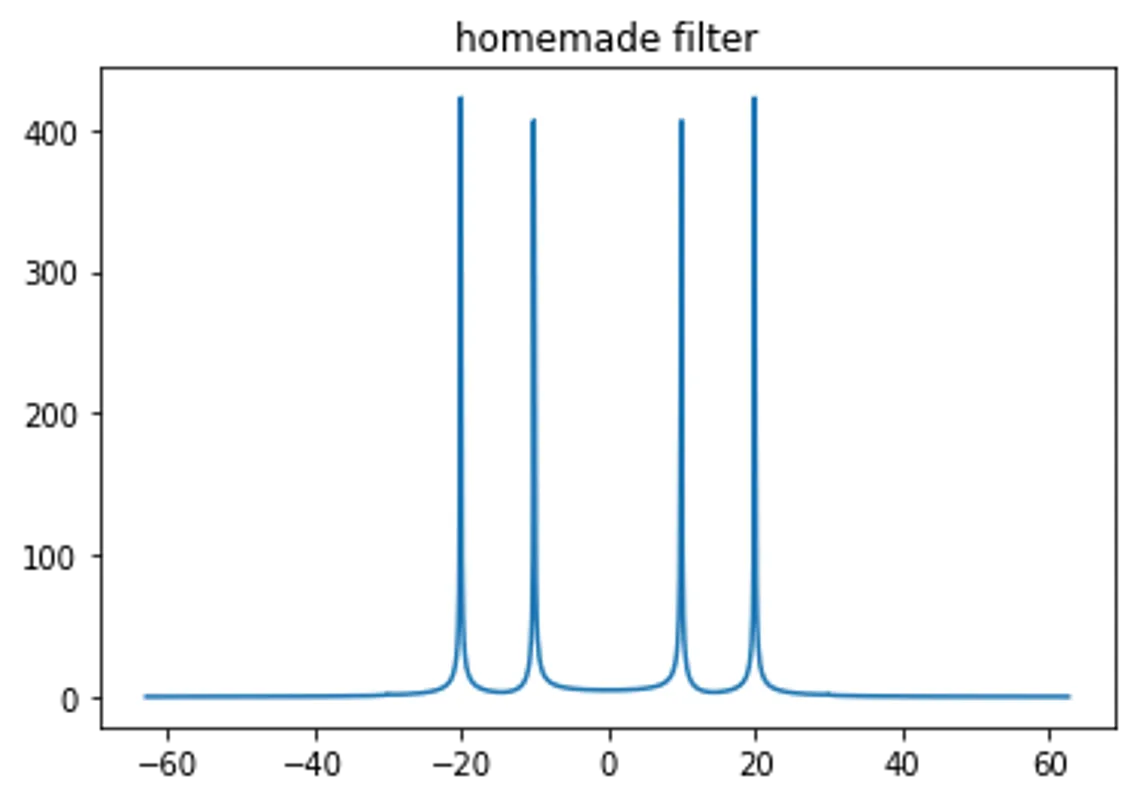
  item = k1/np.pi*np.sum(f_x*np.sinc(k1/np.pi*(xi-x)))
  f_x_filtered.append(item)
f_x_filtered = np.array(f_x_filtered)
plt.plot(x,f_x_filtered); plt.show()

F_k_numpy = dx*np.fft.fft(f_x_filtered)
F_k_numpy = np.concatenate((F_k_numpy[int(N/2):],F_k_numpy[:int(N/2)] ))
plt.title("homemade filter"); plt.plot(k, np.abs(F_k_numpy)); plt.show()

# numpy
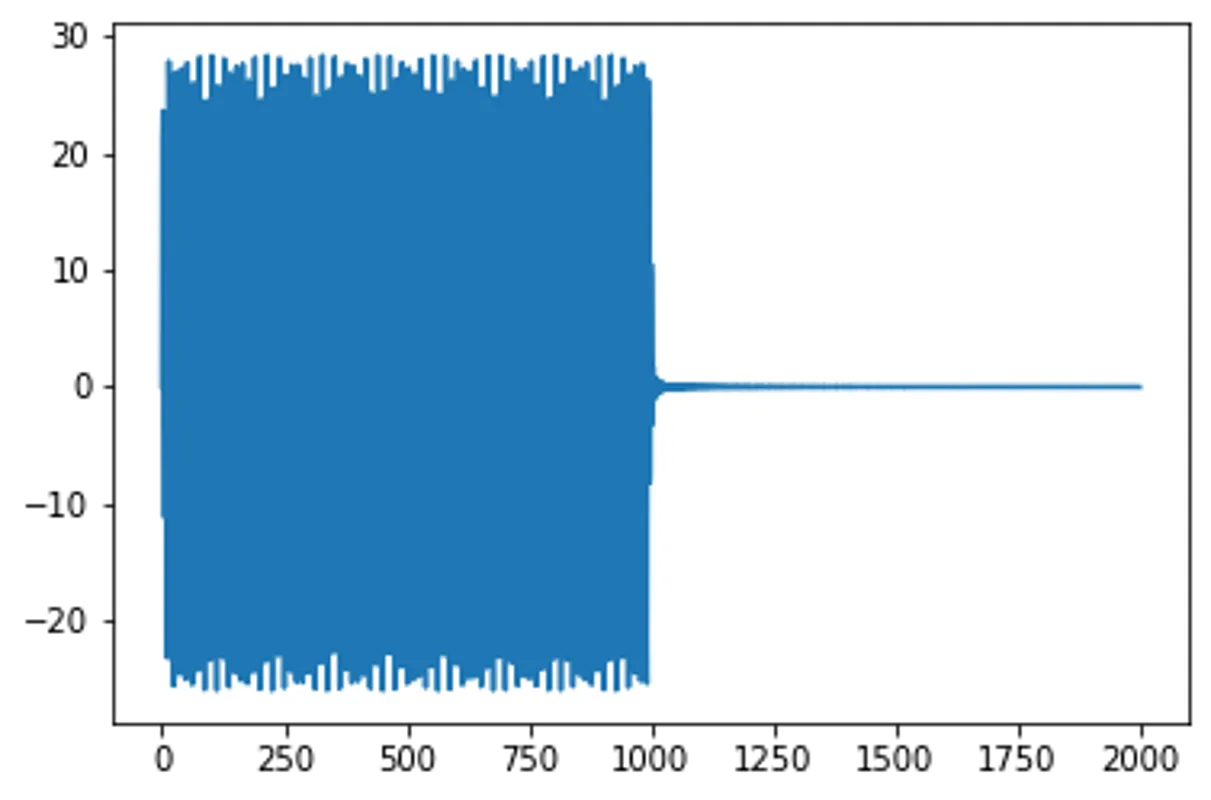
sinc = np.sinc(k1/np.pi * x)
f_x_filtered = k1/np.pi * np.convolve(f_x,sinc)
plt.plot(f_x_filtered); plt.show()
f_x_filtered = f_x_filtered[:N]

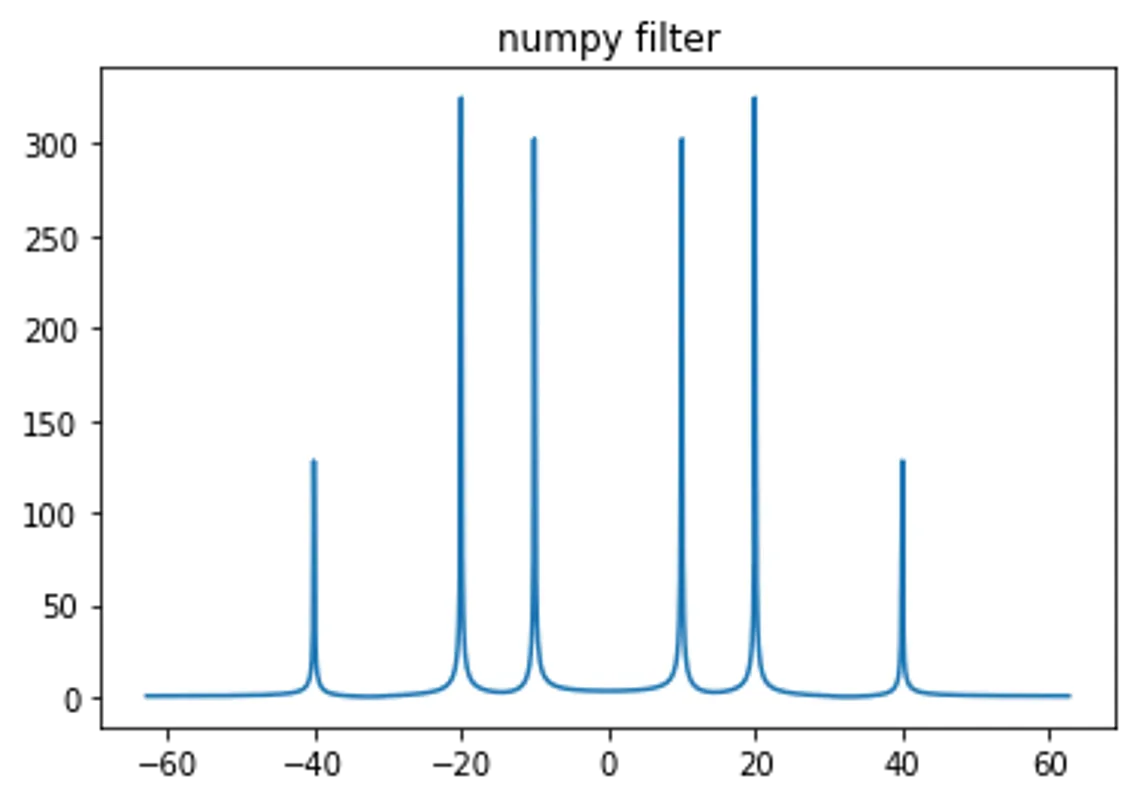
F_k_numpy = dx*np.fft.fft(f_x_filtered)
F_k_numpy = np.concatenate((F_k_numpy[int(N/2):],F_k_numpy[:int(N/2)] ))
plt.title("numpy filter"); plt.plot(k, np.abs(F_k_numpy)); plt.show()