CODE 1D DPFT Momentum Space

Thomas Fermi Approximation

\[\begin{split}E_1^{TF}[T-\mu]=g\int {drdp\over (2\pi)^3}[ T(p)+V_{\text{ext}}(r)-\mu ]\eta(\mu -T-V_{\text{ext}}) \\ \Rightarrow \rho={\delta E_1^{TF} \over \delta T}= g\int {dr \over (2\pi)^3} 1\cdot \eta(\mu -T-V_{\text{ext}})\\ = g{1 \over (2\pi)^3} {4\over 3}\pi R^3={g \over 6\pi^3}R^3 \\ \text{Where }R \text{ is the radius of the sphere such that } \mu -T-V_{\text{ext}}>0\end{split}\]

  • For harmonic oscillator in 1D, and ignore the various constants, we have

\[\begin{split}V=x^2\Rightarrow \mu -T- x^2>0 \Rightarrow x < \sqrt{\mu-T}\equiv R\\ \Rightarrow \rho= g{1 \over 2\pi} 2R ={g \over \pi} \sqrt{\mu-T}\end{split}\]

Effective Kinetic Envergy \(T\)

\[\begin{split}T(p)={\delta \over \delta \rho}E_{\text{int}} +T_{\text{kin}}\\ \text{where } T_{\text{kin}} = {1\over 2}p^2\end{split}\]

The Interaction

  • I don’t know what \(E_{\text{int}}\) should look like at the moment, let just assume the same form as in [1D DPFT In Python] so that

\[T_{\text{int}} = { \delta E_{\text{int}} \over \delta \rho}= w \rho\]

Why momentum space ?

  • As can be seen above, in position space, we have fixed expression for density \(n=\sqrt{\alpha^{-1}[\mu - V_{\text{ext}}]}\), this expression does not change, only \(V_{\text{ext}}\) changes

  • In momentum space

  • We start with \(\mu -T- V_{\text{ext}}(r)>0\) , then

    \(R=V_{\text{ext}}^{\text{Inv}}(\mu-T)\) and \(\rho = {g\over 6\pi^3}R^3\)

  • The position space and momentum space are only equivalent, at least computationally, for harmonic oscillators! And this is a result of the fundamental relation \(T={1\over 2}p^2\)

  • Therefore, depends on \(V_{\text{ext}}\), some problem may be easier to solve in momentum space!

Simple DPFT in Momentum space (Hamonic Oscillator 1D)

import numpy as np
import matplotlib.pyplot as plt

class SimpleDPFT:
  def __init__(self,args):
    self.Tkin = args["Tkin"]
    self.maxIteration = args["maxIteration"]
    self.mu = args["mu"]
    self.g = args["g"]
    self.N = args["N"]
    self.dp = args["dp"]
    self.learningRate = args["learningRate"]
    self.gradientMax = args["gradientMax"]
    self.w = args["w"]
    self.p = args["p"]
    self.nChangeMax = args["nChangeMax"]

  def selfConsistentLoop(self):
    self.T = self.Tkin
    self.mu = self.enforceN(self.mu)
    self.n = self.getDensity(self.mu)
    for i in range(self.maxIteration):
      self.T = self.Tkin + self.w * self.n
      self.mu = self.enforceN(self.mu)
      nOld = self.n
      self.n = (1-self.p)*self.n + self.p*self.getDensity(self.mu)
      if(np.sum(abs(self.n-nOld))<self.nChangeMax):
        break
    return self.n

  def enforceN(self, mu):
    # gradient descent
    for i in range(self.maxIteration):
      gradient = (self.cost(mu+1)-self.cost(mu))
      mu = mu - self.learningRate * gradient
      if(abs(gradient)<self.gradientMax):
        break
    return mu
  def cost(self, mu):
    return abs(self.N - np.sum(self.getDensity(mu)*self.dp) )

  def getDensity(self,mu):
    muMinusT = mu - self.T
    muMinusT[ muMinusT<0 ] = 0
    return self.g/np.pi * np.sqrt(muMinusT)

  # == Bisection ================
  def enforceN(self):
    muNmin = muNmax = 1
    while(self.getN(muNmin)>self.N):
      muNmin = muNmin/2
    while(self.getN(muNmax)<self.N):
      muNmax = muNmax*2
    for i in range(self.maxIteration):
      middlePoint = (muNmin+muNmax)/2
      if(self.getN(middlePoint)>self.N):
        muNmax = middlePoint
      else:
        muNmin = middlePoint
      if(self.getN(muNmin)/self.getN(muNmax)>(1-1e-3)):
        break
    return muNmin

  def getN(self,mu):
    return np.sum(self.getDensity(mu)*self.dp)

# =================================================
# ================= Usage =========================
# =================================================
p = np.linspace(-10, 10, num=100)
dp = p[1]-p[0]
args = {
    "Tkin": p**2/2,
    "maxIteration": 4000,
    "mu": 1,
    "g": 1,
    "N": 20,
    "dp": dp,
    "learningRate": 1e-1,
    "gradientMax": 1e-6,
    "w": 5,
    "p": 0.5,
    "nChangeMax": 1e-6,
}

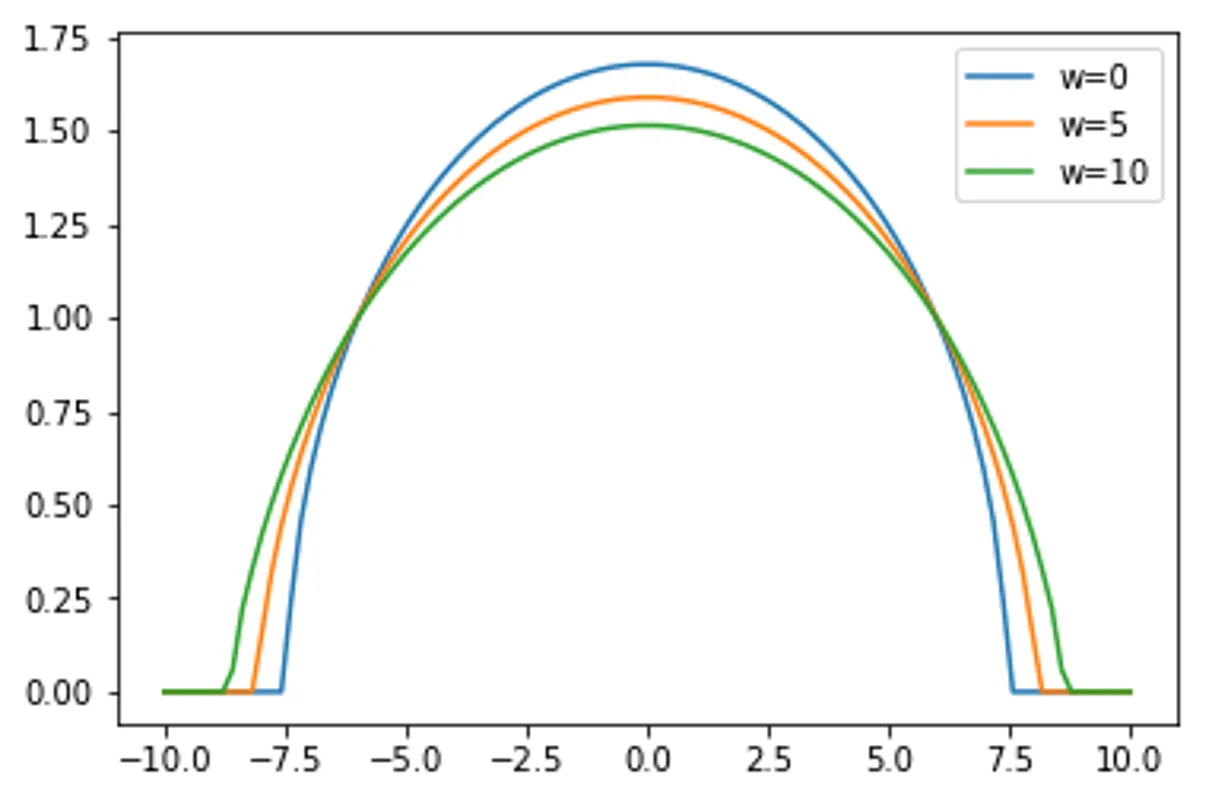
for w in range(3):
  args["w"] = w*5
  simpleDPFT = SimpleDPFT(args)
  n = simpleDPFT.selfConsistentLoop()
  print("Particle Number Check:", np.sum(n)*dp,"/ 20")
  plt.plot(p,n,label="w="+str(w*5))
plt.legend()
plt.show()

Particle Number Check: 19.65459900651429 / 20
Particle Number Check: 19.560823172965314 / 20
Particle Number Check: 19.494538379097083 / 20
../_images/output_6_1.webp

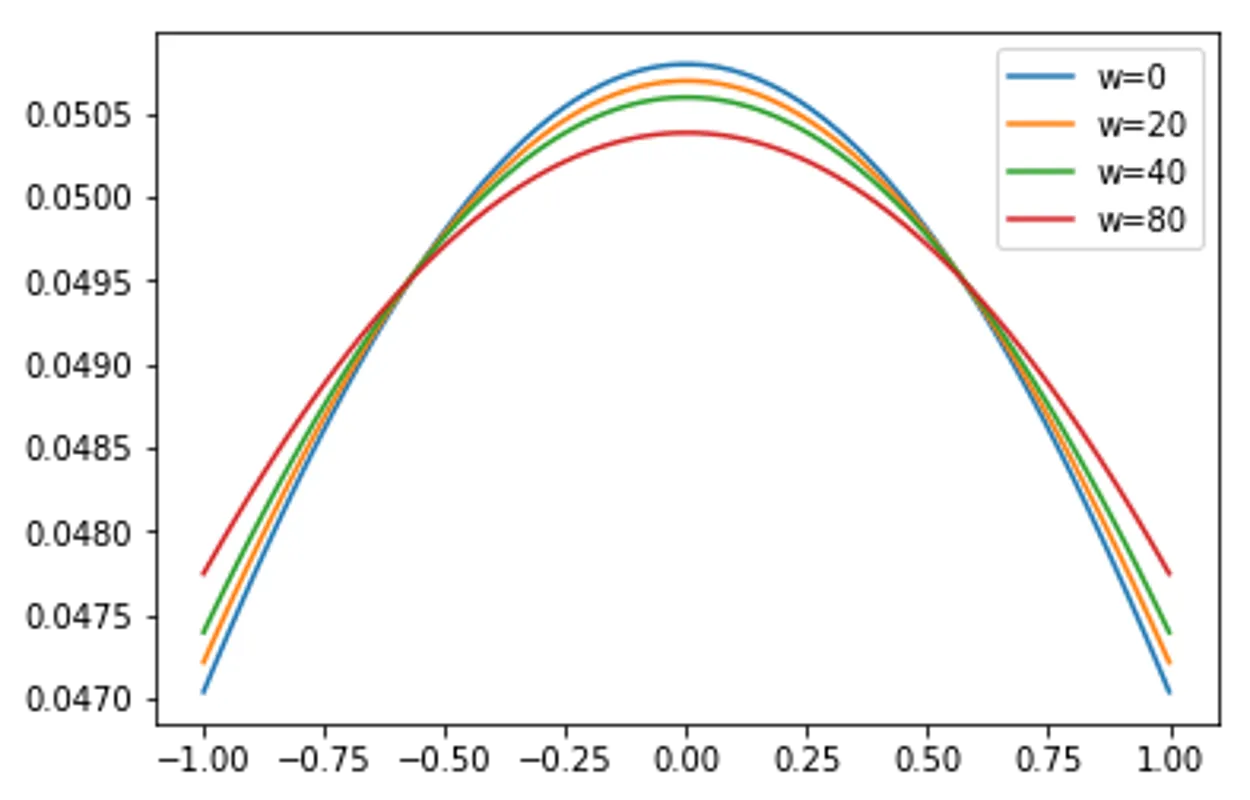
Simple DPFT in Momentum space (Coulomb potential 1D)

\({Z\over T-\mu}>r, \text{ Then }\rho = {g\over \pi}{Z\over T-\mu}\)

Gradient descent doesn’t work for Coulomb potential, so we use Bisection

import numpy as np
import matplotlib.pyplot as plt

class SimpleDPFT:
  def __init__(self,args):
    self.p = args["p"]
    self.g = args["g"]
    self.N = args["N"]
    self.w = args["w"]
    self.mixRatio = args["mixRatio"]
    self.maxIteration=args["maxIteration"]

    self.Tkin = self.p**2/2
    self.dp = self.p[1] - self.p[0]

  def selfConsistentLoop(self):
    self.T = self.Tkin
    self.mu = self.enforceN()
    self.n = self.getDensity(self.mu)
    for i in range(self.maxIteration):
      self.T = self.T + self.w * self.n
      self.mu = self.enforceN()
      nOld = self.n
      self.n = (1-self.mixRatio)*self.n \
              + self.mixRatio   *self.getDensity(self.mu)
      ratio = self.n/nOld
      if(np.sum(ratio)/ratio.shape[0] < (1+1e-3) \
         and np.sum(ratio)/ratio.shape[0] > (1-1e-3)):
        break
    return self.n

  def enforceN(self):
    # mu must be negative
    # if abs(mu)*2, TminusMu increase, N decrease
    muNmin = muNmax = -1
    while(self.getN(muNmin) > self.N):
      muNmin = muNmin*2
    while(self.getN(muNmax) < self.N):
      muNmax = muNmax/2
      if(muNmax==0):
        print("Max N you can get with such w:", self.getN(muNmax))
        assert False, "Your N is not achievable since w is too large!"
    for i in range(self.maxIteration):
      middlePoint = (muNmin+muNmax)/2
      if(self.getN(middlePoint)>self.N):
        muNmax = middlePoint
      else:
        muNmin = middlePoint
      if(self.getN(muNmin)/self.getN(muNmax)>(1-1e-3)):
        break
    return muNmin

  def getN(self,mu):
    return np.sum(self.getDensity(mu)*self.dp)

  def getDensity(self,mu):
    return self.g/np.pi/(self.T-mu)

# =================================================
# ================= Usage =========================
# =================================================
p = np.linspace(-1,1,num=100)
N = 0.1
args = {
    "p":p,
    "g":1,
    "N":N,
    "mixRatio":0.5,
    "maxIteration":1000,
}

wList = [0,20,40,80]
for w in wList:
  args["w"] = w
  simpleDPFT = SimpleDPFT(args)
  n = simpleDPFT.selfConsistentLoop()
  print("Particle Number Check:",np.sum(n)*(p[1]-p[0]),"/",N)
  plt.plot(p,n,label="w="+str(w))
plt.legend()
plt.show()

Particle Number Check: 0.09995211570740857 / 0.1
Particle Number Check: 0.0999575484394774 / 0.1
Particle Number Check: 0.09996421750569122 / 0.1
Particle Number Check: 0.09994714485865916 / 0.1
../_images/output_8_1.webp